文章目录

Ch12. 无穷级数(一) 常数项级数正项级数交错级数任意项级数4个特殊的常数项级数收敛级数的性质（针对任意项级数）常数项级数的审敛法1.正项级数审敛法2.交错级数审敛法 —— 莱布尼茨收敛定理3.常用于举反例的一般项 (二) 幂级数阿贝尔定理泰勒级数（麦克劳林级数）0.求 幂级数的 收敛半径、收敛区间、收敛域1.函数→幂级数 ：函数 f ( x ) f(x) f(x)展开为幂级数2.幂级数→函数：求 和函数S(x) (三) 傅里叶级数三角级数傅里叶级数、傅里叶系数正弦级数、余弦级数狄利克雷收敛定理奇延拓、偶延拓、周期延拓

Ch12. 无穷级数

(一) 常数项级数

正项级数

交错级数

任意项级数

4个特殊的常数项级数

①等比级数

②p级数

③调和级数
∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + . . . + 1 n + . . . = ∞ \sum\limits_{n=1}^∞\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{n}+...=∞ n=1∑∞​n1​=1+21​+31​+...+n1​+...=∞       发散

④交错调和级数
交错调和级数：收敛
交错p级数：收敛

收敛级数的性质（针对任意项级数）

(1)(2)加减数乘都收敛

---

例题：06年9.

分析：ABC仅对正项级数成立。
举反例：
AB： a n = ( − 1 ) n ⋅ 1 n a_n=(-1)^n·\dfrac{1}{n} an​=(−1)n⋅n1​

C： a n = ( − 1 ) n ⋅ 1 n a_n=(-1)^n·\dfrac{1}{\sqrt{n}} an​=(−1)n⋅n ​1​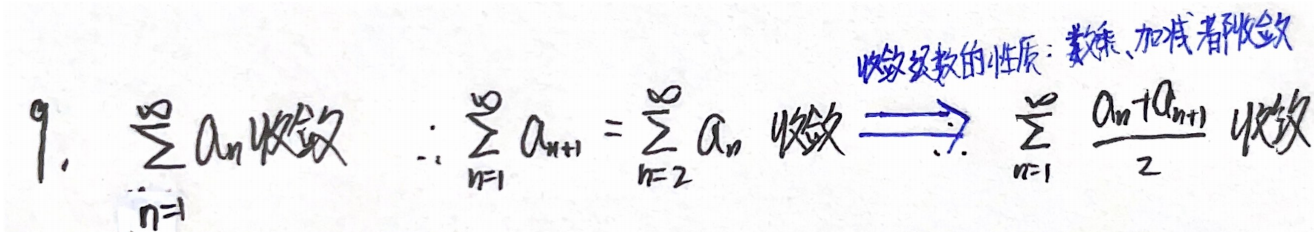

答案：D

---

常数项级数的审敛法

1.正项级数审敛法

①充要条件

②比较审敛法
大的收敛，小的收敛；
小的发散，大的发散。

---

例题：09年4.  正项级数的比较审敛法、举反例

分析：
对于A，取 a n = b n = ( − 1 ) n 1 n a_n=b_n=(-1)^n\dfrac{1}{\sqrt{n}} an​=bn​=(−1)nn ​1​，则 a n b n = 1 n a_nb_n=\dfrac{1}{n} an​bn​=n1​，为调和级数，发散

对于C，用正项级数的比较审敛法证明C正确： lim ⁡ n → ∞ a n 2 b n 2 ∣ b n ∣ = lim ⁡ n → ∞ a n 2 ∣ b n ∣ = 0 ∴ ∣ b n ∣ \lim\limits_{n→∞}\dfrac{a_n^2b_n^2}{|b_n|}=\lim\limits_{n→∞}a_n^2|b_n|=0 \quad ∴|b_n| n→∞lim​∣bn​∣an2​bn2​​=n→∞lim​an2​∣bn​∣=0∴∣bn​∣更大。由比较审敛法，大的收敛，则小的 a n 2 b n 2 a_n^2b_n^2 an2​bn2​必收敛

答案：C

---

③比较审敛法极限形式

④比值法
ρ = lim ⁡ n → ∞ u n + 1 u n { ρ < 1 ，收敛 ρ > 1 ，发散 ρ = 1 ，不定，可能收敛可能发散 ρ=\lim\limits_{n→∞}\dfrac{u_{n+1}}{u_n} \qquad \qquad \left\{\begin{aligned} ρ & < 1，收敛 \\ ρ & > 1，发散 \\ ρ & =1，不定，可能收敛可能发散 \end{aligned}\right. ρ=n→∞lim​un​un+1​​⎩ ⎨ ⎧​ρρρ​<1，收敛>1，发散=1，不定，可能收敛可能发散​

⑤根值法

⑥极限审敛法

⑦积分判别法

⑧A-D判别法(任意项级数)

⑨绝对收敛必收敛 (任意项级数)

2.交错级数审敛法 —— 莱布尼茨收敛定理

莱布尼茨收敛定理：
若交错级数 ∑ n = 1 ∞ ( − 1 ) n − 1 u n \sum_{n=1}^∞(-1)^{n-1}u_n ∑n=1∞​(−1)n−1un​ 满足 u n u_n un​单调递减趋于0，则交错级数收敛
即满足 (1) u n ≥ u n + 1 u_n≥u_{n+1} un​≥un+1​  (2) lim ⁡ n → ∞ u n = 0 \lim\limits_{n→∞}u_n=0 n→∞lim​un​=0.

---

例题：11年2.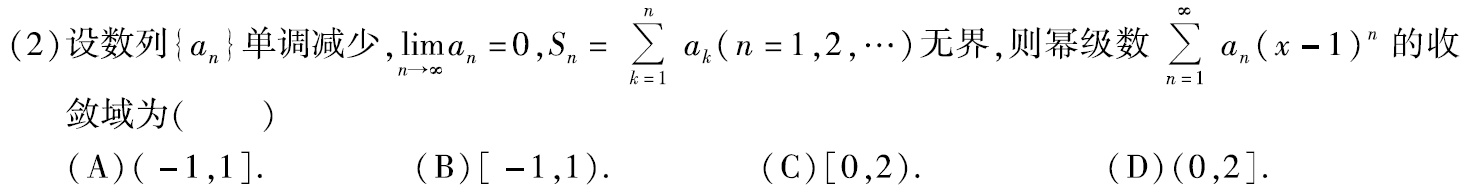

分析：显然 ∑ n = 1 ∞ a n ( x − 1 ) n \sum\limits_{n=1}^∞a_n(x-1)^n n=1∑∞​an​(x−1)n 的收敛中心为 x=1，故排除AB
代入x=2，得发散，所以2处应该为开区间，选C

答案：C

---

3.常用于举反例的一般项

a n = 1 n a_n=\dfrac{1}{n} an​=n1​ 或 a n = ( − 1 ) n ⋅ 1 n a_n=(-1)^n·\dfrac{1}{n} an​=(−1)n⋅n1​

a n = ( − 1 ) n ⋅ 1 n a_n=(-1)^n·\dfrac{1}{\sqrt{n}} an​=(−1)n⋅n ​1​

---

例题：09年4.

---

(二) 幂级数

e x = ∑ k = 0 ∞ x k k ! e^x=\sum\limits_{k=0}^∞\dfrac{x^k}{k!} ex=k=0∑∞​k!xk​

∴ e = ∑ k = 0 ∞ 1 k ! = lim ⁡ x → ∞ ( 1 + 1 x ) x ∴e=\sum\limits_{k=0}^∞\dfrac{1}{k!}=\lim\limits_{x→∞}(1+\dfrac{1}{x})^x ∴e=k=0∑∞​k!1​=x→∞lim​(1+x1​)x

---

例题：10年14.   数字特征与幂级数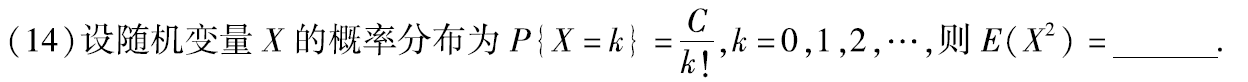

答案：2

---

阿贝尔定理

当|x|<R时，幂级数绝对收敛；
当|x|>R时，幂级数发散；
当x = R或x = -R时，幂级数敛散性不定，可能收敛也可能发散.

正数R称为幂级数的收敛半径。开区间(-R,R)称为幂级数的收敛区间。

---

例题：11年2.

---

泰勒级数（麦克劳林级数）

1 + x + x 2 + x 3 + . . . + x n + . . . = 1 1 − x = ∑ n = 0 ∞ x n ( − 1 < x < 1 ) 1 − x + x 2 − x 3 + . . . + ( − 1 ) n x n + . . . = 1 1 + x = ∑ n = 0 ∞ ( − 1 ) n x n ( − 1 < x < 1 ) e x = ∑ n = 0 ∞ 1 n ! x n ( − ∞ < x < + ∞ ) 1+x+x²+x³+...+x^n+...=\dfrac{1}{1-x}=\sum\limits_{n=0}^∞x^n \qquad (-1<x<1)\\[5mm] 1-x+x^2-x^3+...+(-1)^nx^n+...=\dfrac{1}{1+x}=\sum\limits_{n=0}^∞(-1)^nx^n \qquad (-1<x<1)\\[5mm] e^x=\sum\limits_{n=0}^∞\dfrac{1}{n!}x^n \qquad (-∞<x<+∞) 1+x+x2+x3+...+xn+...=1−x1​=n=0∑∞​xn(−1<x<1)1−x+x2−x3+...+(−1)nxn+...=1+x1​=n=0∑∞​(−1)nxn(−1<x<1)ex=n=0∑∞​n!1​xn(−∞<x<+∞)

0.求 幂级数的 收敛半径、收敛区间、收敛域

1.收敛半径R：
ρ = lim ⁡ n → ∞ ∣ a n + 1 a n ∣ R = 1 ρ ρ=\lim\limits_{n→∞}|\dfrac{a_{n+1}}{a_n}|\qquad \qquad R=\dfrac{1}{ρ} ρ=n→∞lim​∣an​an+1​​∣R=ρ1​
2.收敛区间： ( − R , R ) (-R,R) (−R,R)         收敛区间是开区间
3.收敛域：在收敛区间的基础上，验证x=R和x=-R两个端点

1.函数→幂级数 ：函数 f ( x ) f(x) f(x)展开为幂级数

函数→幂级数：
①凑标杆：先求导或积分到标杆 1 1 − x \dfrac{1}{1-x} 1−x1​ 的形式 (x可以为任意形式)，以“标杆”为桥梁变成幂级数 ∑ n = 0 ∞ x n \sum\limits_{n=0}^{∞}x^n n=0∑∞​xn (x可以为任意形式)。
②凑题干：和分两项，尽力合并，注意题干是n=0还是n=1，努力把两项变一项，凑成题干的形式
③求常数项级数：此时的求常数项级数，就是把幂级数中的x代入特定值。

---

例题1：01年13.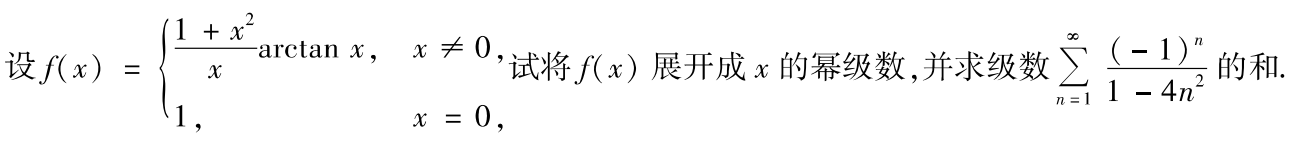

分析：

答案： π 4 − 1 2 \dfrac{π}{4}-\dfrac{1}{2} 4π​−21​

---

2.幂级数→函数：求 和函数S(x)

1.会标杆：重要的展开式
2.幂级数求导和积分要会

1.重要“标杆”：
∑ n = 0 ∞ x n = 1 + x + x 2 + x 3 + . . . + x n + . . . = 1 1 − x ( − 1 < x < 1 ) \sum\limits_{n=0}^∞x^n=1+x+x²+x³+...+x^n+...=\dfrac{1}{1-x} \qquad (-1<x<1) n=0∑∞​xn=1+x+x2+x3+...+xn+...=1−x1​(−1<x<1)
及其变形:
∑ n = 1 ∞ x n = x + x 2 + x 3 + . . . + x n + . . . = x 1 − x ( − 1 < x < 1 ) ∑ n = 0 ∞ ( − 1 ) n x n = 1 − x + x 2 − x 3 + . . . + ( − 1 ) n x n + . . . = 1 1 + x ( − 1 < x < 1 ) \sum\limits_{n=1}^∞x^n=x+x²+x³+...+x^n+...=\dfrac{x}{1-x} \qquad (-1<x<1)\\[3mm] \sum\limits_{n=0}^∞(-1)^nx^n=1-x+x^2-x^3+...+(-1)^nx^n+...=\dfrac{1}{1+x} \qquad (-1<x<1) n=1∑∞​xn=x+x2+x3+...+xn+...=1−xx​(−1<x<1)n=0∑∞​(−1)nxn=1−x+x2−x3+...+(−1)nxn+...=1+x1​(−1<x<1)

---

例题1：05年16.  求收敛区间、和函数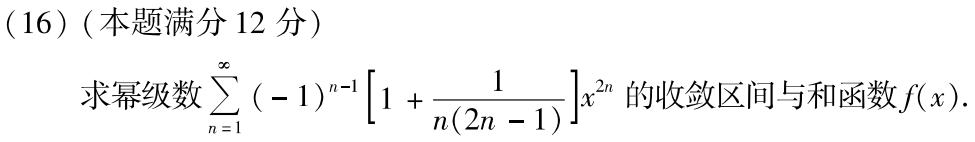

答案：

---

(三) 傅里叶级数

三角级数

形如下式的级数叫做三角级数
a 0 2 + ∑ n = 1 ∞ ( a n cos ⁡ n π t l ) + b n sin ⁡ n π t l ) \frac{a_0}{2}+\sum_{n=1}^∞(a_n\cos\frac{nπt}{l})+b_n\sin\frac{nπt}{l}) 2a0​​+n=1∑∞​(an​coslnπt​)+bn​sinlnπt​)

令 π t l = x \dfrac{πt}{l}=x lπt​=x，三角级数可变为
a 0 2 + ∑ n = 1 ∞ ( a n cos ⁡ n x ) + b n sin ⁡ n x ) \frac{a_0}{2}+\sum_{n=1}^∞(a_n\cos nx)+b_n\sin nx) 2a0​​+n=1∑∞​(an​cosnx)+bn​sinnx)
这就把以 2 l 2l 2l 为周期的三角级数转换成以 2 π 2π 2π 为周期的三角级数。

傅里叶级数、傅里叶系数

傅里叶级数：
a 0 2 + ∑ n = 1 ∞ ( a n cos ⁡ n x ) + b n sin ⁡ n x ) \frac{a_0}{2}+\sum_{n=1}^∞(a_n\cos nx)+b_n\sin nx) 2a0​​+n=1∑∞​(an​cosnx)+bn​sinnx)

傅里叶系数：
{ a n = 1 π ∫ − π π f ( x ) cos ⁡ n x d x ( n = 0 , 1 , 2 , 3 , . . . ) b n = 1 π ∫ − π π f ( x ) sin ⁡ n x d x ( n = 1 , 2 , 3 , . . . ) \left\{\begin{aligned} a_n=\frac{1}{π}\int_{-π}^{π}f(x)\cos nx{\rm d}x \quad (n=0,1,2,3,...)\\ b_n=\frac{1}{π}\int_{-π}^{π}f(x)\sin nx{\rm d}x \qquad (n=1,2,3,...) \end{aligned}\right. ⎩ ⎨ ⎧​an​=π1​∫−ππ​f(x)cosnxdx(n=0,1,2,3,...)bn​=π1​∫−ππ​f(x)sinnxdx(n=1,2,3,...)​

正弦级数、余弦级数

已知傅里叶系数为：
{ a n = 1 π ∫ − π π f ( x ) cos ⁡ n x d x ( n = 0 , 1 , 2 , 3 , . . . ) b n = 1 π ∫ − π π f ( x ) sin ⁡ n x d x ( n = 1 , 2 , 3 , . . . ) \left\{\begin{aligned} a_n=\frac{1}{π}\int_{-π}^{π}f(x)\cos nx{\rm d}x \quad (n=0,1,2,3,...)\\ b_n=\frac{1}{π}\int_{-π}^{π}f(x)\sin nx{\rm d}x \qquad (n=1,2,3,...) \end{aligned}\right. ⎩ ⎨ ⎧​an​=π1​∫−ππ​f(x)cosnxdx(n=0,1,2,3,...)bn​=π1​∫−ππ​f(x)sinnxdx(n=1,2,3,...)​

①当 f ( x ) 为奇函数 f(x)为奇函数 f(x)为奇函数时， f ( x ) cos ⁡ n x f(x)\cos nx f(x)cosnx是奇函数， f ( x ) sin ⁡ n x f(x)\sin nx f(x)sinnx是偶函数，故
{ a n = 0 ( n = 0 , 1 , 2 , 3 , . . . ) b n = 2 π ∫ 0 π f ( x ) sin ⁡ n x d x ( n = 1 , 2 , 3 , . . . ) \left\{\begin{aligned} a_n=0 \qquad \qquad \qquad \qquad (n=0,1,2,3,...)\\ b_n=\frac{2}{π}\int_0^{π}f(x)\sin nx{\rm d}x \quad (n=1,2,3,...) \end{aligned}\right. ⎩ ⎨ ⎧​an​=0(n=0,1,2,3,...)bn​=π2​∫0π​f(x)sinnxdx(n=1,2,3,...)​

②当 f ( x ) 为偶函数 f(x)为偶函数 f(x)为偶函数时， f ( x ) cos ⁡ n x f(x)\cos nx f(x)cosnx是偶函数， f ( x ) sin ⁡ n x f(x)\sin nx f(x)sinnx是奇函数，故
{ a n = 2 π ∫ 0 π f ( x ) cos ⁡ n x d x ( n = 0 , 1 , 2 , 3 , . . . ) b n = 0 ( n = 1 , 2 , 3 , . . . ) \left\{\begin{aligned} a_n=\frac{2}{π}\int_0^{π}f(x)\cos nx{\rm d}x \qquad (n=0,1,2,3,...)\\ b_n =0 \qquad \qquad \qquad \qquad \quad \qquad (n=1,2,3,...) \end{aligned}\right. ⎩ ⎨ ⎧​an​=π2​∫0π​f(x)cosnxdx(n=0,1,2,3,...)bn​=0(n=1,2,3,...)​

即知
奇函数的傅里叶级数是只含有正弦项的正弦级数： ∑ n = 1 ∞ b n sin ⁡ n x \sum\limits_{n=1}^∞b_n\sin nx n=1∑∞​bn​sinnx

偶函数的傅里叶级数是只含有余弦项的余弦级数： a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n x \dfrac{a_0}{2}+\sum\limits_{n=1}^∞a_n\cos nx 2a0​​+n=1∑∞​an​cosnx

---

例题1：03年3.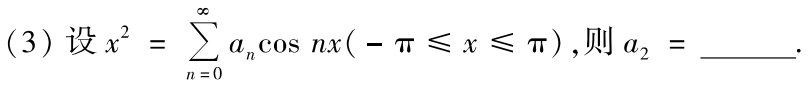

分析：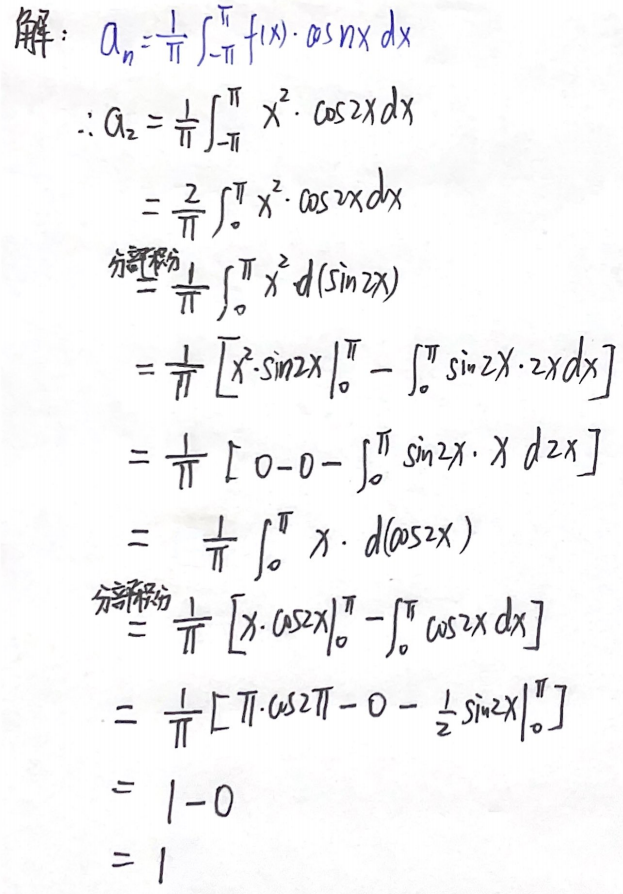

答案：1

---

狄利克雷收敛定理

设f(x)是周期为2π的周期函数，若它满足：
(1)在一个周期内连续或只有有限个第一类间断点
(2)在一个周期内至多只有有限个极值点

那么f(x)的傅里叶级数收敛，并且
①当x是f(x)的连续点时，级数收敛于f(x) 和函数S(x)=f(x)
②当x是f(x)的间断点时，级数收敛于 1 2 [ f ( x − ) + f ( x + ) ] \dfrac{1}{2}[f(x^-)+f(x^+)] 21​[f(x−)+f(x+)] 和函数S(x)=间断点左右极限的平均值

奇延拓、偶延拓、周期延拓

奇延拓：把(0,π]上的奇函数延展为(-π,π]上的奇函数
偶延拓：把(0,π]上的偶函数延展为(-π,π]上的偶函数
周期延拓：从周期为(-π,π] 延展为周期为2π的周期函数

---

例题：13年3.   奇延拓、周期延拓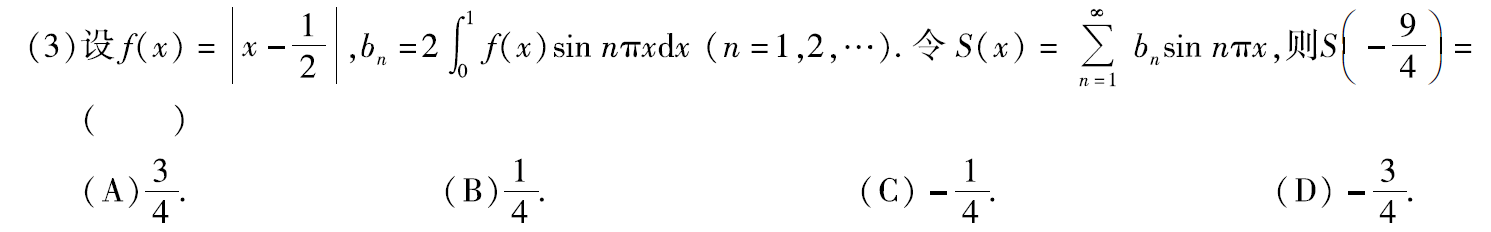

分析：S(x)表达式为正弦函数，说明是奇函数的傅里叶级数，f(x)为奇函数。
观察bn，知x∈(0,1)
对f(x)进行奇延拓，周期延拓，则f(x)周期为2
∴ S ( − 9 4 ) = S ( − 9 4 + 2 ) = S ( − 1 4 ) = f ( − 1 4 ) = − 1 4 ∴S(-\frac{9}{4})=S(-\frac{9}{4}+2)=S(-\frac{1}{4})=f(-\frac{1}{4})=-\frac{1}{4} ∴S(−49​)=S(−49​+2)=S(−41​)=f(−41​)=−41​

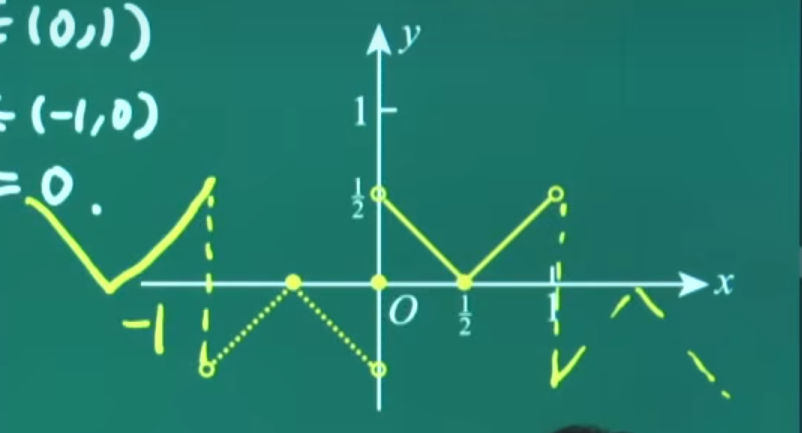
答案：C

---