写在前面

由于代码较长，csdn对文章总长度有字数限制，想只看完整代码的请移步另一篇博客。

https://blog.csdn.net/qq_46640863/article/details/125735894

目录

写在前面一、实验内容二、实验目的三、实验分析四、实验流程4.1 整体流程4.2 构造DFA4.3 用分析表分析 五、实验代码5.1 数据结构5.2 部分核心算法设计5.3 完整程序 六、运行结果七、实验感悟

一、实验内容

1.实现LR(0)分析算法
2.输入：文法 E → a A ∣ b B A → c A ∣ d B → c B ∣ d \begin{matrix}E\to aA|bB\\A\to cA|d\\B\to cB|d\end{matrix} E→aA∣bBA→cA∣dB→cB∣d​，待分析的语句（例如acccd）
3.输出：语句的分析过程（参见ppt例题）
4.要求：LR(0)分析表程序自动生成。如果使用已知的分析表，实验分数会降低。

二、实验目的

通过设计、编制、调试一个具体的文法分析程序，深入理解LR(0)预测分析法的基本分析原理，学会自动生成LR(0)分析表，并利用分析表对输入语句进行分析。

三、实验分析

待分析文法示例如下：
G [ E ] ( 1.1 ) E → a A ∣ b B A → c A ∣ d B → c B ∣ d G[E](1.1)\\ E\to aA|bB\\ A\to cA|d\\ B\to cB|d G[E](1.1)E→aA∣bBA→cA∣dB→cB∣d
为了识别唯一的“接受”状态，并消除”|”符号，需要对文法进行增广，增广后的文法为：
G [ E ] ( 1.2 ) S → E E → a A E → b B A → c A A → d B → c B B → d G[E](1.2)\\ S\to E\\ E\to aA\\ E\to bB\\ A\to cA\\ A\to d\\ B\to cB\\ B \to d G[E](1.2)S→EE→aAE→bBA→cAA→dB→cBB→d
对文法中每一个产生式的右部添加一个圆点·，称为文法的一个LR(0)项目（简称项目）。一个项目指明了在分析过程中某个时刻我们能看到产生式多大一部分。圆点“·”指出了分析过程中扫描输入串的当前位置。圆点“·”前的部分为已经扫描过的符号串，圆点“·”后的部分为待扫描的符号串，且圆点“·”前的符号串构成了一个活前缀。圆点在最右端的项目为“规约”项目，圆点“·”右侧第一个符号是终结符称为“移进”项目。圆点“·”右侧第一个符号是非终结符称为“待约”项目。
1. S → ⋅ E S \to ·E S→⋅E
2. S → E ⋅ S\to E· S→E⋅
3. E → ⋅ a A E\to ·aA E→⋅aA
4. E → a ⋅ A E\to a·A E→a⋅A
5. E → a A ⋅ E\to aA· E→aA⋅
6. E → ⋅ b B E\to ·bB E→⋅bB
7. E → b ⋅ B E\to b·B E→b⋅B
8. E → b B ⋅ E\to bB· E→bB⋅
9. A → ⋅ c A A\to ·cA A→⋅cA
10. A → c ⋅ A A\to c·A A→c⋅A
11. A → c A ⋅ A\to cA· A→cA⋅
12. A → ⋅ d A\to ·d A→⋅d
13. A → d ⋅ A\to d· A→d⋅
14. B → ⋅ c B B\to ·cB B→⋅cB
15. B → c ⋅ B B\to c·B B→c⋅B
16. B → c B ⋅ B\to cB· B→cB⋅
17. B → ⋅ d B\to ·d B→⋅d
18. B → d ⋅ B\to d· B→d⋅
使用闭包项方法把识别活前缀的NFA确定化，成为一个以项目集为状态的DFA，这个项目集（状态）为项目集规范族。用 ϵ _ C L O S U R E \epsilon \_CLOSURE ϵ_CLOSURE办法构造项目集规范族。假定I是文法的任一项目集，则构造I的闭包 ϵ _ C L O S U R E ( I ) \epsilon \_CLOSURE(I) ϵ_CLOSURE(I)的方法是：
1.I的任何项目都属于CLOSURE(I)。
2.若 A → a ⋅ B β A\to a·B\beta A→a⋅Bβ属于CLOSURE(I)，那么对任何关于B的产生式 B → γ B\to\gamma B→γ，其项目 B → ⋅ γ B\to ·\gamma B→⋅γ也属于CLOSURE(I)
3.重复执行上述(1)~(2)步直到不再增大为止。
用 ϵ _ C L O S U R E \epsilon \_CLOSURE ϵ_CLOSURE办法构造文法 G [ S ] ( 1.2 ) G[S](1.2) G[S](1.2)的LR(0)项目集规范族如下：

构造该文法的DFA。对于一个项目集来说，除了规约项目之外，对于其余移进项目，“·”之后有多少个不同的字符，就要引出多少条有向边到不同的项目集。在项目集中根据某一项目“·”后的首字符，引出有向边到达另一项目集，要分两种情况考虑：一种是项目在目前已存在的所有项目集均未出现，则引出有向边到达一新产生的项目集，该项目集纳入新项目。另一种是项目在目前已存在的项目集中某一个已经出现，则不产生新的项目集。
本实验中，文法的DFA M如下图：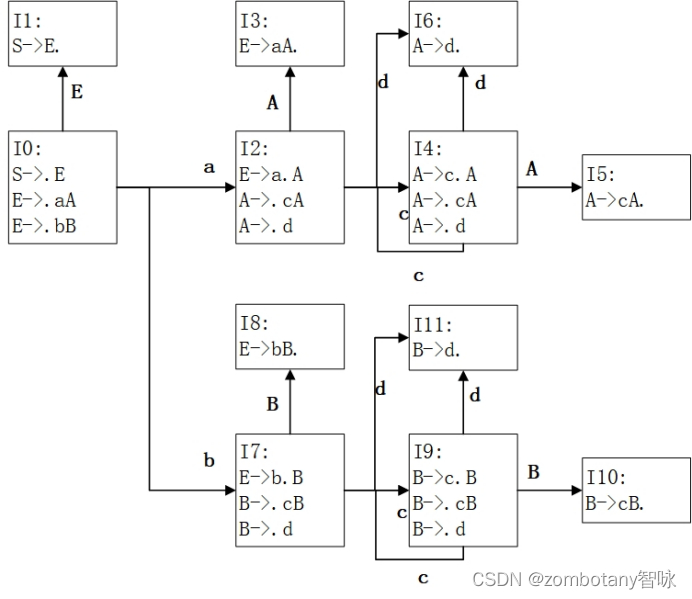

根据DFA构造LR(0)分析表的方法如下：在每个不同 I i I_i Ii​的都分别对应一行且将这些不同的 I i I_i Ii​的下标 i i i依次标记在该行的第一列上以表示不同的状态行。ACTION表中相对于文法每一个终结符（包括终结符#）都对应一列，而GOTO表则相对文法的每一个终结符（除 S ′ S' S′外）都对应一列。对于每一个 I i I_i Ii​，如果 I i I_i Ii​发出的有向边上标记的是终结符且该有向边指向 I k I_k Ik​，则在ACTION表的第 i i i行及该终结符这一列所对应的栏中填上 s k s_k sk​。如果有向边上标记的是非终结符且该有向边指向 I k I_k Ik​，则在GOTO表的第 i i i行及该非终结符这一列所对应的栏中填上 k k k。如果 I i I_i Ii​中含有规约项目，并且拓广文法中产生式序号为 j j j，则ACTION表的第 i i i行全部填入 r j r_j rj​。如果 I i I_i Ii​是含有形如 S ′ → S S'\to S S′→S这样的规约项目，则第 i i i行对应的ACTION表终结符#这一列栏中填入“acc”

状态	a	b	c	d	#	S	E	A	B
0	s2	s7					1
1					acc
2			s4	s6				3
3	r1	r1	r1	r1	r1
4			s4	s6				5
5	r3	r3	r3	r3	r3
6	r4	r4	r4	r4	r4
7			s9	s11					8
8	r2	r2	r2	r2	r2
9			s9	s11					10
10	r5	r5	r5	r5	r5
11	r6	r6	r6	r6	r6

在分析时，每一项 A C T I O N [ s , a ] ACTION[s,a] ACTION[s,a]所规定的的动作是以下四种情况之一：
（1）移进：使栈顶状态 s s s与当前扫描的输入符号 a a a（终结符）的下一状态 s ′ = A C T I O N [ s , a ] s'=ACTION[s,a] s′=ACTION[s,a]进栈，而下一个输入符号则变成当前扫描的输入符号。
（2）规约：如果符号栈栈顶的符号串为 α \alpha α，且文法中存在 A → α A\to \alpha A→α，则将栈顶的符号串 α \alpha α用非终结符 A A A替换，将 α \alpha α规约为 A A A。对状态栈来说，假定 α \alpha α长度 γ \gamma γ，则状态栈栈顶 γ \gamma γ个状态序列恰好识别符号串 α \alpha α，此时可用产生式 A → α A\to\alpha A→α规约。假定原来 s m s_m sm​为栈顶状态，则此时 s m − γ s_{m-\gamma} sm−γ​为新的栈顶状态，使 s m − γ s_{m-\gamma} sm−γ​与所规约的非终结符 A A A的下一个状态 s ′ = G O T O [ s m − γ , A ] s'=GOTO[s_{m-\gamma},A] s′=GOTO[sm−γ​,A]和 A A A分别进入状态栈和符号栈。规约状态不改变当前扫描的输入符号。
（3）接受：分析工作成功，所分析的句子被文法识别，分析器停止工作。
（4）报错：发现所分析的句子不是文法允许的句子。
对于符号串“acccd”，分析过程如下表所示。

步骤	状态栈	符号栈	输入串	动作
1	0	#	acccd#	S2:状态2入栈
2	02	#a	cccd#	S4:状态4入栈
3	024	#ac	ccd#	S4:状态4入栈
4	0244	#acc	cd#	S4:状态4入栈
5	02444	#accc	d#	S6:状态6入栈
6	024446	#acccd	#	r4:用 A → d A\to d A→d规约,6出栈, G O T O [ 4 , A ] = 5 GOTO[4,A]=5 GOTO[4,A]=5
7	024445	#acccA	#	r3:用 A → c A A\to cA A→cA规约,45出栈, G O T O [ 4 , A ] = 5 GOTO[4,A]=5 GOTO[4,A]=5
8	02445	#accA	#	r3:用 A → c A A\to cA A→cA规约,45出栈, G O T O [ 4 , A ] = 5 GOTO[4,A]=5 GOTO[4,A]=5
9	0245	#acA	#	r3:用 A → c A A\to cA A→cA规约,45出栈, G O T O [ 4 , A ] = 5 GOTO[4,A]=5 GOTO[4,A]=5
10	023	#aA	#	r1:用 E → a A E\to aA E→aA规约,23出栈, G O T O [ 0 , E ] = 1 GOTO[0,E]=1 GOTO[0,E]=1
11	01	#E	#	ACC：接受，分析成功。

四、实验流程

4.1 整体流程

从文件中读取文法，对其进行增广，消除”|”后，识别出终结符与非终结符。
对第0条产生式生成 ϵ _ C L O S U R E \epsilon\_{CLOSURE} ϵ_CLOSURE。之后递归的根据此构造出每个状态，并形成一个DFA。与书上手动地用广度优先遍历构造状态的顺序不同，本实验为了简化，深度优先遍历的顺序构造DFA。这一个步骤在求DFA的过程中，填入了LR0分析表的GOTO和移进项目。
在求出了每个项目和项目集规范族后，再次遍历所有状态。若当前项目为规约项目，则判断当前是不是形如 S → E S\to E S→E的项目。若是，则遇到#后接受符号串，ACC。否则，为规约项目，根据产生式进行规约。
这一步填入了规约项目。
输出分析表，输入字符串，并对输入的字符串进行分析。
所以，本次实验的整体流程图如下：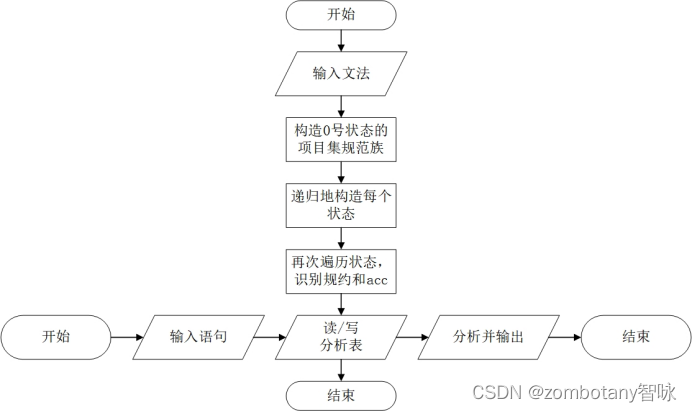

4.2 构造DFA

以递归的顺序对第0条产生式的 ϵ _ C L O S U R E \epsilon\_{CLOSURE} ϵ_CLOSURE中的每一个项目移进并生成该项目的 ϵ _ C L O S U R E \epsilon\_{CLOSURE} ϵ_CLOSURE，对每个项目集规范族中的每个项目继续移进、继续递归地生成新的项目集规范族，生成新的状态。直到生成的项目为规约项目，递归终止。在移进的过程中，若当前符号是非终结符，则记录GOTO下一状态。若当前符号是终结符，则记录shift下一状态。GOTO和shift时，都需要判断下一状态是否已经被构造过了。
为了简化流程，本实验不判断移进-规约冲突。因为输入的文法本身也不存在移进-规约冲突。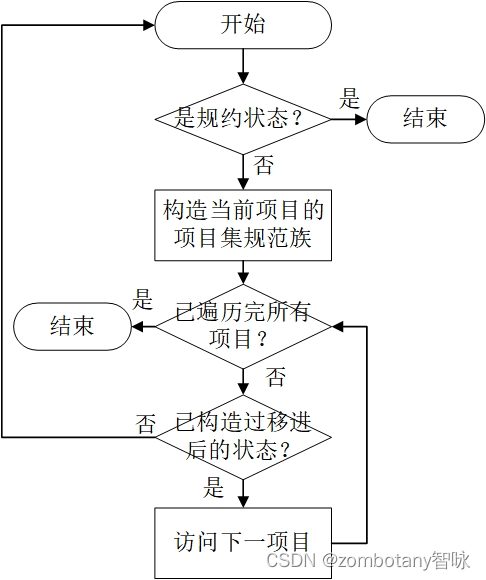

4.3 用分析表分析

首先，需要对输入串中加入“#”号。之后反复地执行如下的流程：
读取状态栈栈顶。读取输入串首字符。如果状态栈和输入串首字符的表项不存在，则出错。否则，根据表项中的内容进行下述步骤：若为“ACC”，则接受，返回。若表项中第一个字符为”s”，则为移进，根据表项中的内容将新的状态入栈，也将符号入栈，指向输入串下一字符。若表项中第一个字符为”r”，则为规约。根据表项中的内容，判断用哪条语句进行规约。计算这条语句产生式右部长度，符号栈和状态栈中都出栈元素，数量为产生式右部长度。根据产生式左部，将产生式的左部重新入符号栈，将状态栈加入该非终结符与栈顶状态的GOTO表项。
分析的流程图如下所示。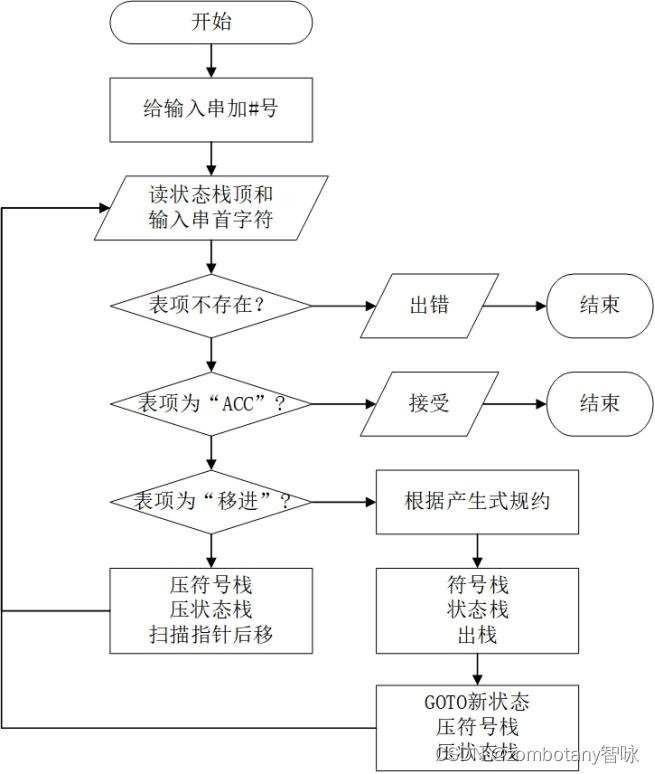

五、实验代码

5.1 数据结构

文法开始符为char S
终结符、非终结符记录在集合中。set<char> VN,VT
用cell记录分析表中的表项。属性为类型、下一个状态id、规约的文法id。

struct cell {motionType mt = UNKNOWN;int nxtsid = -1;int gid = -1;};

Table为分析表本体
cell table[100][100];
为了方便读取，需要将字符和编号互相转化。
map<char, int> charToId;
char idToChar[100];
Gright为每个产生式的右部，键值为产生式左部。因为每个非终结符对应不止一个产生式，所以用vector存储。G为产生式本体。Grammer类也用于记录每条产生式。

map<char, vector<int>> Gright;vector<pair<char, string>> G;class grammer {public:int gid;char left;string right;};vector<grammer> Gs;

item为文法中的项目

struct item {int gid;int i = 0;    // 圆点在第i个字符前};    // 项目及项目的状态

State为由项目集规范族构成的状态

class state {public:int sid;bool end = false;vector<item> Is;    // 该状态下的所有项目set<char> right_VNs;}vector<state> Ss;

5.2 部分核心算法设计

求解某个项目的项目集规范族（ ϵ _ C L O S U R E \epsilon\_CLOSURE ϵ_CLOSURE），重新遍历每一条产生式，判断产生式左部是否为当前项目的圆点“·”右部的非终结符。若是，则加入。

bool findMore() {if (end) return false;bool found = false;for (auto& p : Is) {if (VN.count(Gs[p.gid].right[p.i]) && !right_VNs.count(Gs[p.gid].right[p.i])) {    // 加入待归约项目right_VNs.insert(Gs[p.gid].right[p.i]);found = true;for (auto& gid : Gright[Gs[p.gid].right[p.i]]) {Is.push_back({ gid, 0 });}}}return found;}

递归地求解DFA。在derivateAll()的效果是找到所有状态，并找到每个状态shift和GOTO的状态。利用derivateState()求解每个状态，在每个状态中对每个项目再次进行移进，构建新的项目。调用findMore()求解这个新项目的项目集规范族，判断当前项目集规范族构成的状态是否出现过，若没出现过则构造新的状态。

int derivateState(int isid, char c);void derivateAll(int sid) {if (Ss[sid].end) return;std::set<char> input_c;for (auto& p : Ss[sid].Is) {input_c.insert(Gs[p.gid].right[p.i]);}for (auto& c : input_c) {int nxtsid = derivateState(sid, c);if (nxtsid == -1) continue;// assert(table[sid][charToId[c]].mt == UNKNOWN);if (VN.count(c)) {    // 是非终结符table[sid][charToId[c]].mt = GOTO;table[sid][charToId[c]].nxtsid = nxtsid;}else {    // 是终结符table[sid][charToId[c]].mt = ADDS;table[sid][charToId[c]].nxtsid = nxtsid;}}}int derivateState(int isid, char c) {if (Ss[isid].end) return -1;state ts;bool isend = false;for (auto& p : Ss[isid].Is) {if (Gs[p.gid].right[p.i] == c) {ts.Is.push_back({ p.gid,p.i + 1 });if (Gs[p.gid].right.length() == p.i + 1) {isend = ts.end = true;}}}if (ts.Is.size() == 0) return -1;ts.findMore();int sid;bool rec = false;if (IsToId.count(ts.Is)) {sid = IsToId[ts.Is];rec = true;}else {IsToId[ts.Is] = sid = scnt++;ts.sid = sid;Ss.push_back(ts);printState(sid);}if (!rec) derivateAll(sid);   return sid;}

对文法进行分析的过程，与上文中的流程图是完全一致的。

stack<int> statusStack;stack<char> symbolStack;void LR0Analysis() {inputStr += '#';int p = 0;cout << endl << inputStr << endl;cout << setw(20) << "状态栈" << setw(20) << "符号栈" << setw(20) << "输入串" << setw(20) << "动作" << endl;statusStack.push(0);symbolStack.push('#');while (1) {int status = statusStack.top();char nextChar = inputStr[p];int nextStatus = -1;if (LRTable[status].count(nextChar)) {string info = LRTable[status][nextChar];display(p,inputStr,info);if (info == "ACC")break;if (info[0] == 's') {//移进状态nextStatus = stoi(info.substr(1));statusStack.push(nextStatus);symbolStack.push(nextChar);p++;}else if (info[0] == 'r') {nextStatus = stoi(info.substr(1));for (int i = 0; i < G[nextStatus].second.size(); i++) {symbolStack.pop();statusStack.pop();}char temp = G[nextStatus].first;symbolStack.push(temp);int s = statusStack.top();statusStack.push(stoi(LRTable[s][temp]));}else {break;}}else {cout << "ERROR";return;}}}

其余的程序段以输入输出、预处理、读写为主，在此不再赘述。

5.3 完整程序

https://blog.csdn.net/qq_46640863/article/details/125735894

六、运行结果

从文件中读取输入文法如下。

对这个文法进行增广，结果如下。增广完成后，识别终结符与非终结符。

输出每个状态。状态与第3章节分析的状态是完全一致的。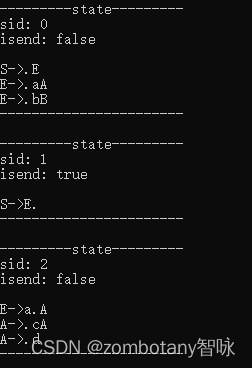




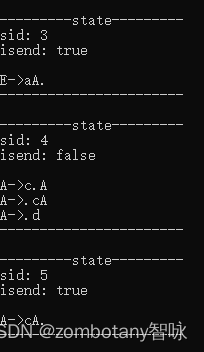
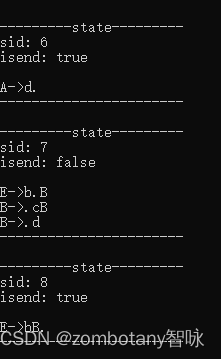
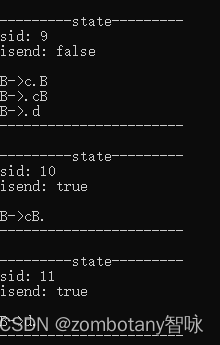
输出分析表。分析表也与第三章节中给出的分析表是一致的，是正确的。

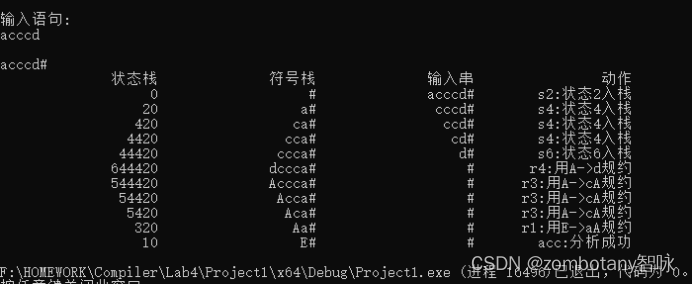
输入语句acccd，自动给出其分析过程。分析过程与第3章节中的实例是完全一致的。正确地对该文法进行了分析。

七、实验感悟